Introduction to Regression
Today’s example will pivot between the content from this week and the example below.
In today’s lecture I will ask you to use real data during the lecture. Please download the following dataset and load it into R (or right-click the address and use that to load into R).
This dataset is from houses in Ames, Iowa. (Thrilling!) We will use this dataset during the lecture to illustrate some of the points discussed below.
We will also use some Atlanta weather data. The Atlanta weather data is linked below:
Preliminaries
For this example, we’re again going to use historical weather data from Dark Sky about wind speed and temperature trends for downtown Atlanta (specifically 33.754557, -84.390009) in 2019. We downloaded this data using Dark Sky’s (about-to-be-retired-because-they-were-bought-by-Apple) API using the darksky package.
If you want to follow along with this example, you can download the data below (you’ll likely need to right click and choose “Save Link As…”):
Code
Load and clean data
First, we load the libraries we’ll be using:
library(tidyverse) # For ggplot, dplyr, and friends
library(patchwork) # For combining ggplot plots
library(GGally) # New one, for scatterplot matrices
library(broom) # For converting model objects to data framesThen we load the data with read_csv(). This is tidyverse’s CSV reader (base R is read.csv). Here we assume that the CSV file was downloaded and lives in a subfolder named data:
weather_atl <- read_csv("data/atl-weather-2019.csv")Legal dual y-axes
It is fine (and often helpful) to use two y-axes if the two different scales measure the same thing, like counts and percentages, Fahrenheit and Celsius, pounds and kilograms, inches and centimeters, etc.
To do this, you need to add an argument (sec.axis) to scale_y_continuous() to tell it to use a second axis. This sec.axis argument takes a sec_axis() function that tells ggplot how to transform the scale. You need to specify a formula or function that defines how the original axis gets transformed. This formula uses a special syntax. It needs to start with a ~, which indicates that it’s a function, and it needs to use . to stand in for the original value in the original axis.
Since the equation for converting Fahrenheit to Celsius is this…
…we can specify this with code like so (where . stands for the Fahrenheit value):
~ (32 - .) * -5 / 9Here’s a plot of daily high temperatures in Atlanta throughout 2019, with a second axis:
ggplot(weather_atl, aes(x = time, y = temperatureHigh)) +
geom_line() +
scale_y_continuous(sec.axis = sec_axis(trans = ~ (32 - .) * -5/9,
name = "Celsius")) +
labs(x = NULL, y = "Fahrenheit") +
theme_minimal()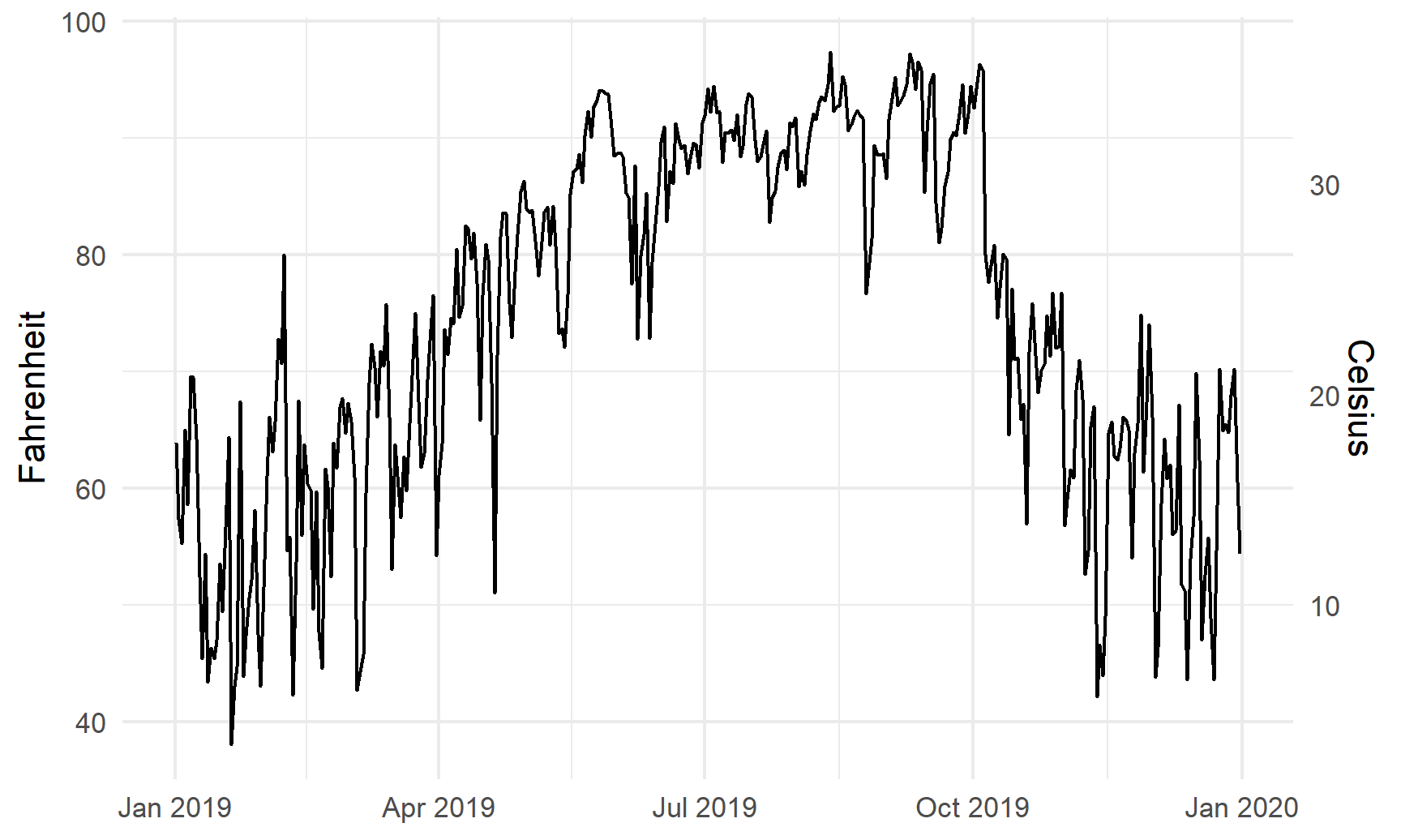
For fun, we could also convert it to Kelvin, which uses this formula:
ggplot(weather_atl, aes(x = time, y = temperatureHigh)) +
geom_line() +
scale_y_continuous(sec.axis = sec_axis(trans = ~ (. - 32) * 5/9 + 273.15,
name = "Kelvin")) +
labs(x = NULL, y = "Fahrenheit") +
theme_minimal()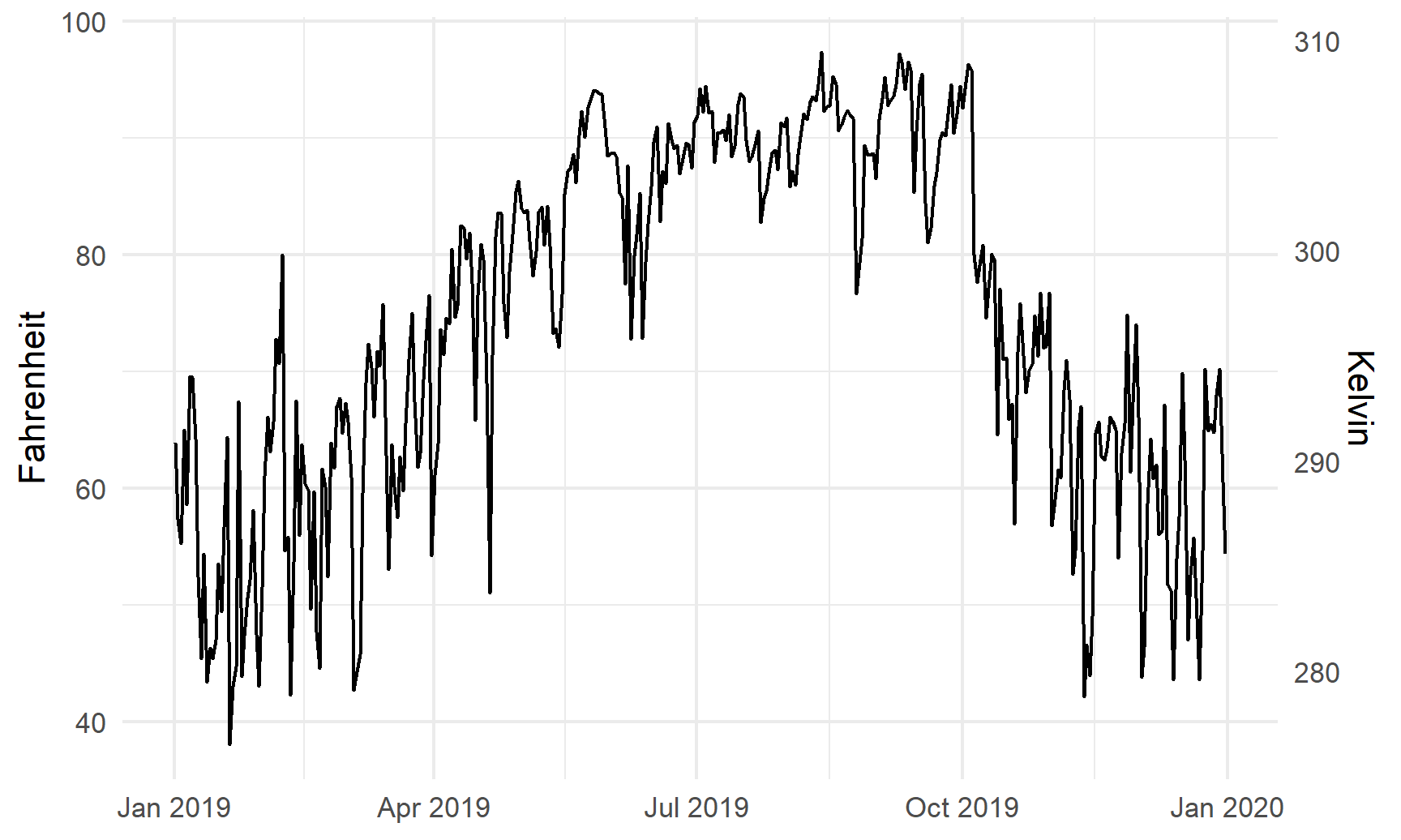
Combining plots
A good alternative to using two y-axes is to use two plots instead. The patchwork package makes this really easy to do with R. There are other similar packages that do this, like cowplot and gridExtra, but I’ve found that patchwork is the easiest to use and it actually aligns the different plot elements like axis lines and legends. The documentation for patchwork is really great and full of examples—you should check it out to see all the things you can do with it!
To use patchwork, we need to (1) save our plots as objects and (2) add them together with +.
For instance, is there a relationship between temperature and humidity in Atlanta? We can plot both:
# Temperature in Atlanta
temp_plot <- ggplot(weather_atl, aes(x = time, y = temperatureHigh)) +
geom_line() +
geom_smooth() +
scale_y_continuous(sec.axis = sec_axis(trans = ~ (32 - .) * -5/9,
name = "Celsius")) +
labs(x = NULL, y = "Fahrenheit") +
theme_minimal()
temp_plot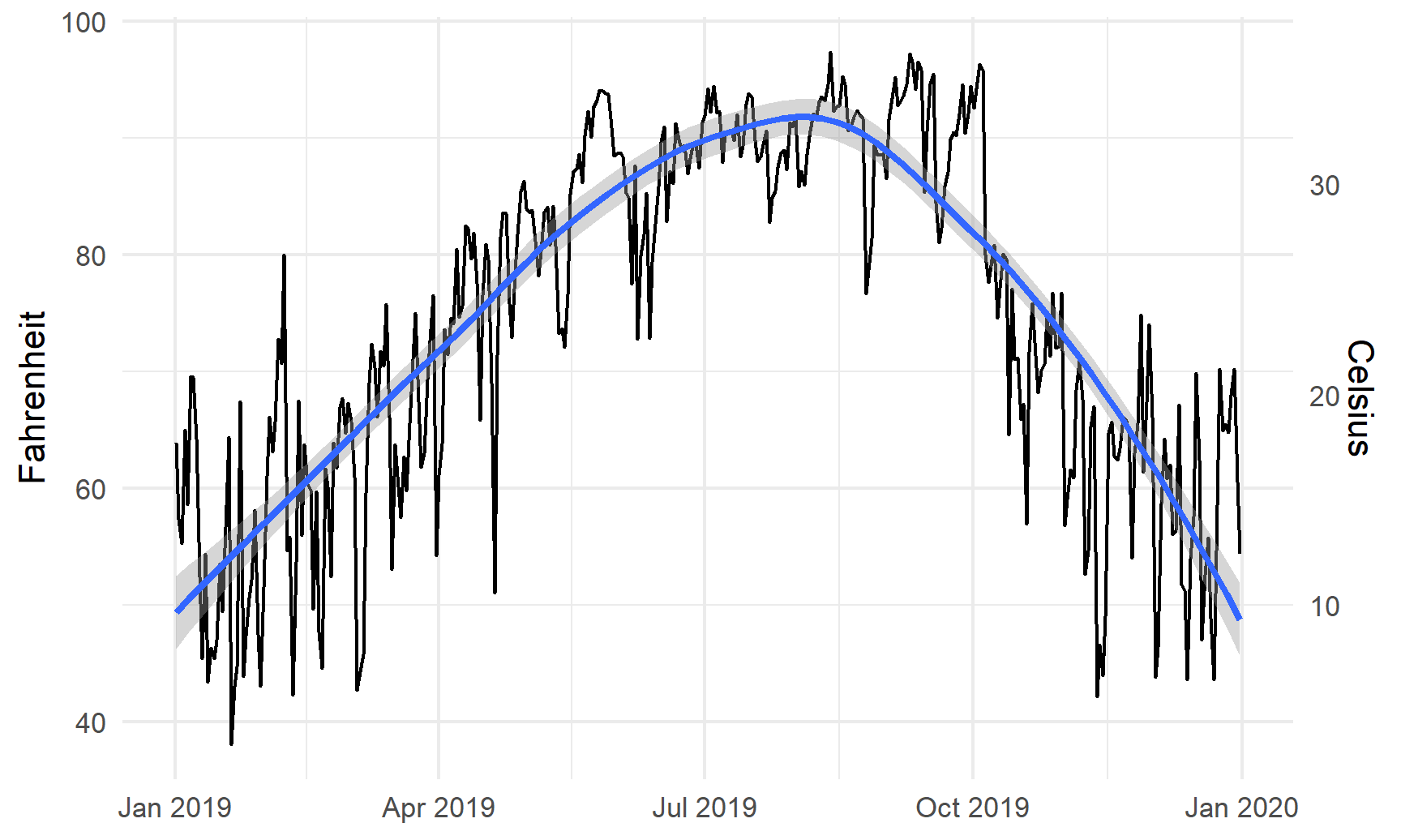
# Humidity in Atlanta
humidity_plot <- ggplot(weather_atl, aes(x = time, y = humidity)) +
geom_line() +
geom_smooth() +
labs(x = NULL, y = "Humidity") +
theme_minimal()
humidity_plot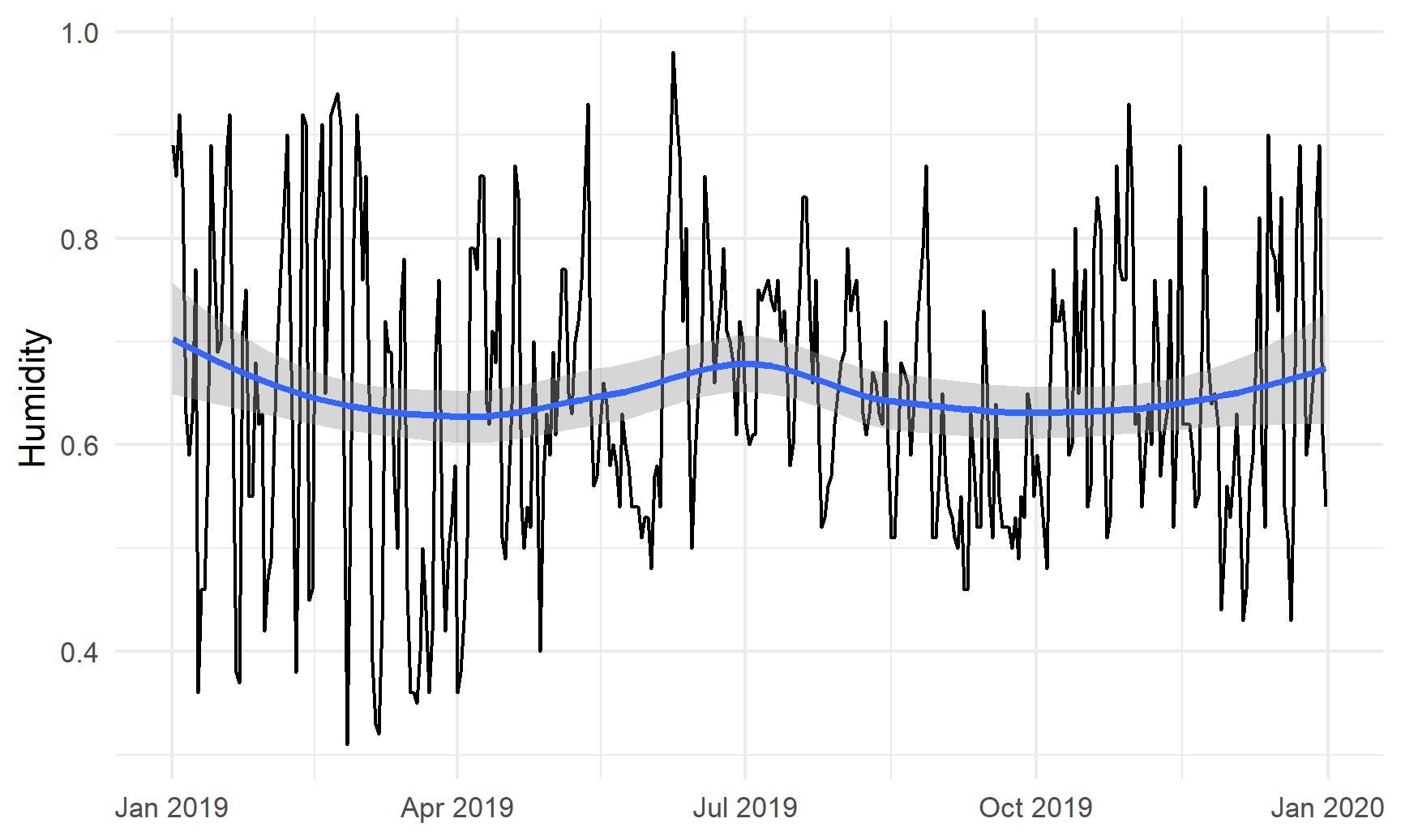
Right now, these are two separate plots, but we can combine them with + if we load patchwork:
library(patchwork)
temp_plot + humidity_plot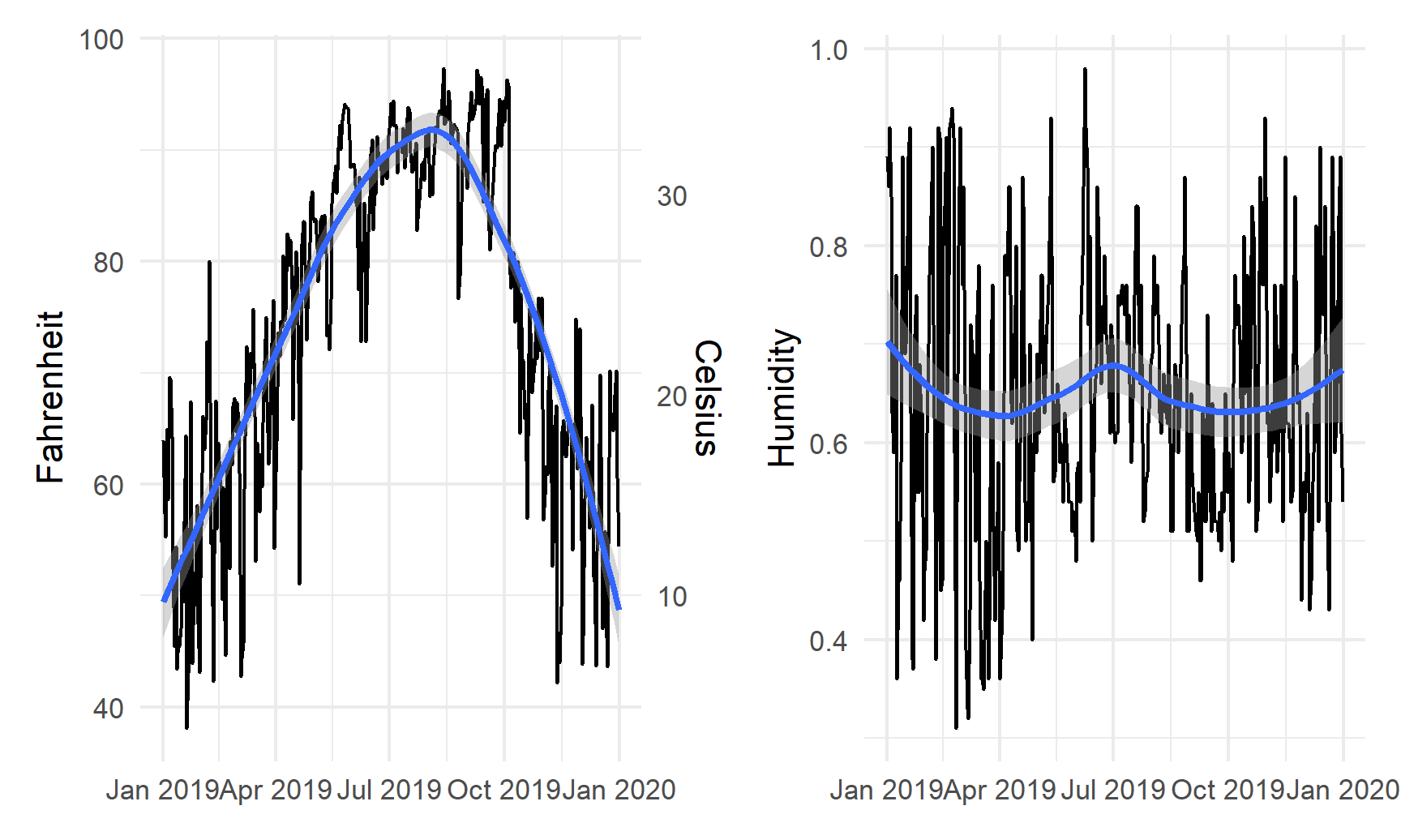
By default, patchwork will put these side-by-side. We can specify that we want the plots to be oriented over/under:
temp_plot / humidity_plot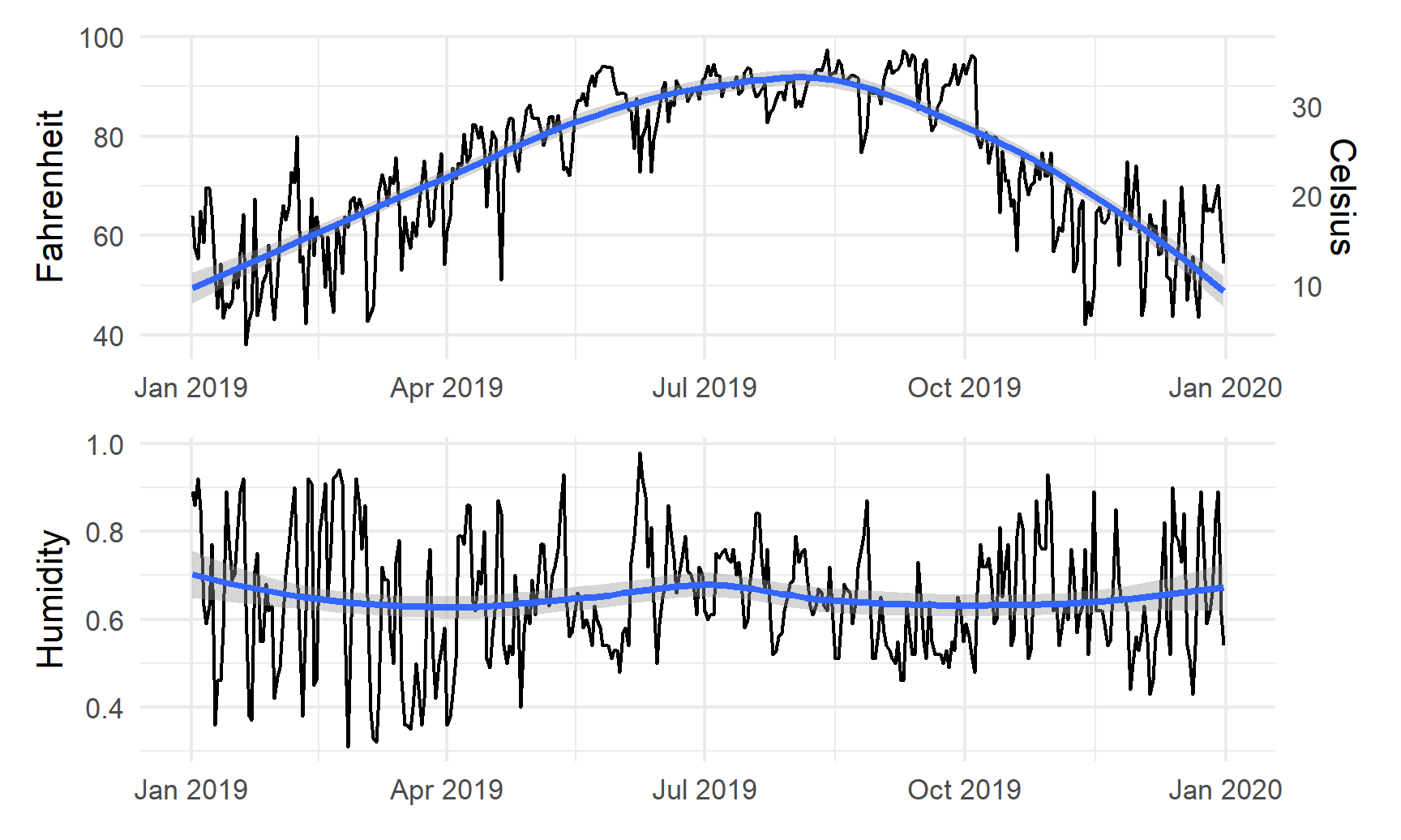
Or we can change the orientation with the plot_layout() function:
temp_plot + humidity_plot +
plot_layout(ncol = 1)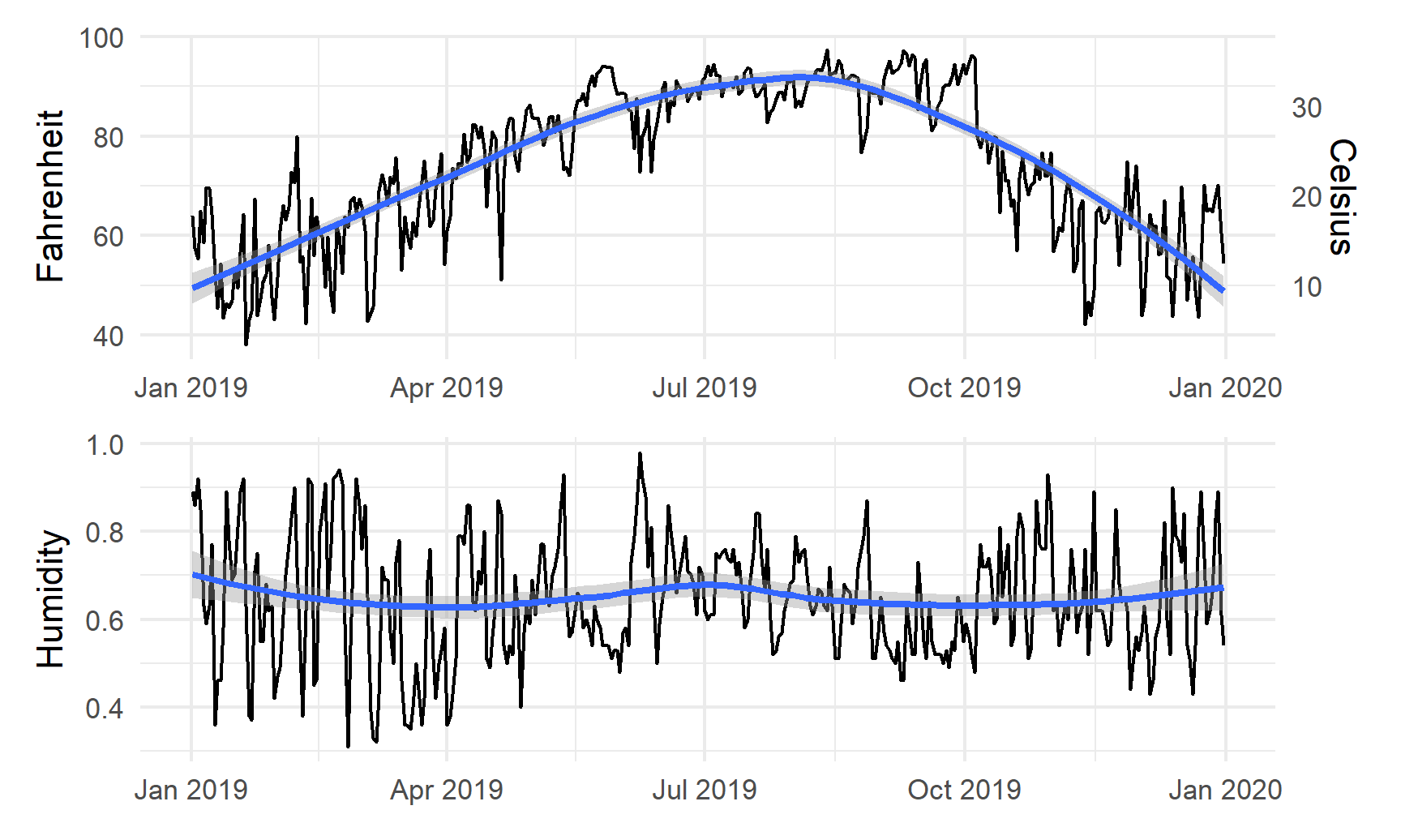
We can also play with other arguments in plot_layout(). If we want to make the temperature plot taller and shrink the humidity section, we can specify the proportions for the plot heights. Here, the temperature plot is 70% of the height and the humidity plot is 30%:
temp_plot + humidity_plot +
plot_layout(ncol = 1, heights = c(0.7, 0.3))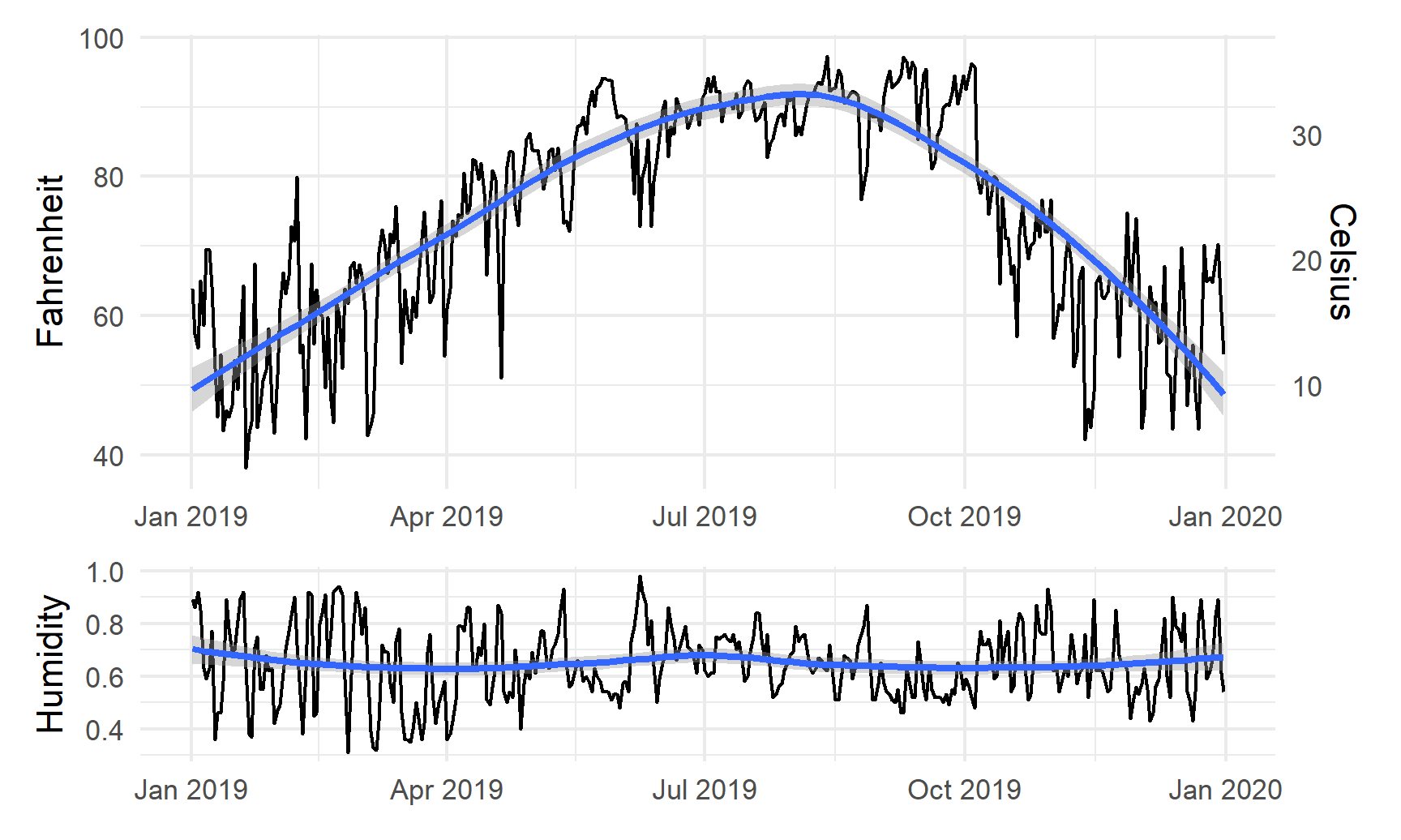
Scatterplot matrices
We can visualize the correlations between pairs of variables with the ggpairs() function in the GGally package. For instance, how correlated are high and low temperatures, humidity, wind speed, and the chance of precipitation? We first make a smaller dataset with just those columns, and then we feed that dataset into ggpairs() to see all the correlation information:
library(GGally)
weather_correlations <- weather_atl %>%
select(temperatureHigh, temperatureLow, humidity, windSpeed, precipProbability)
ggpairs(weather_correlations)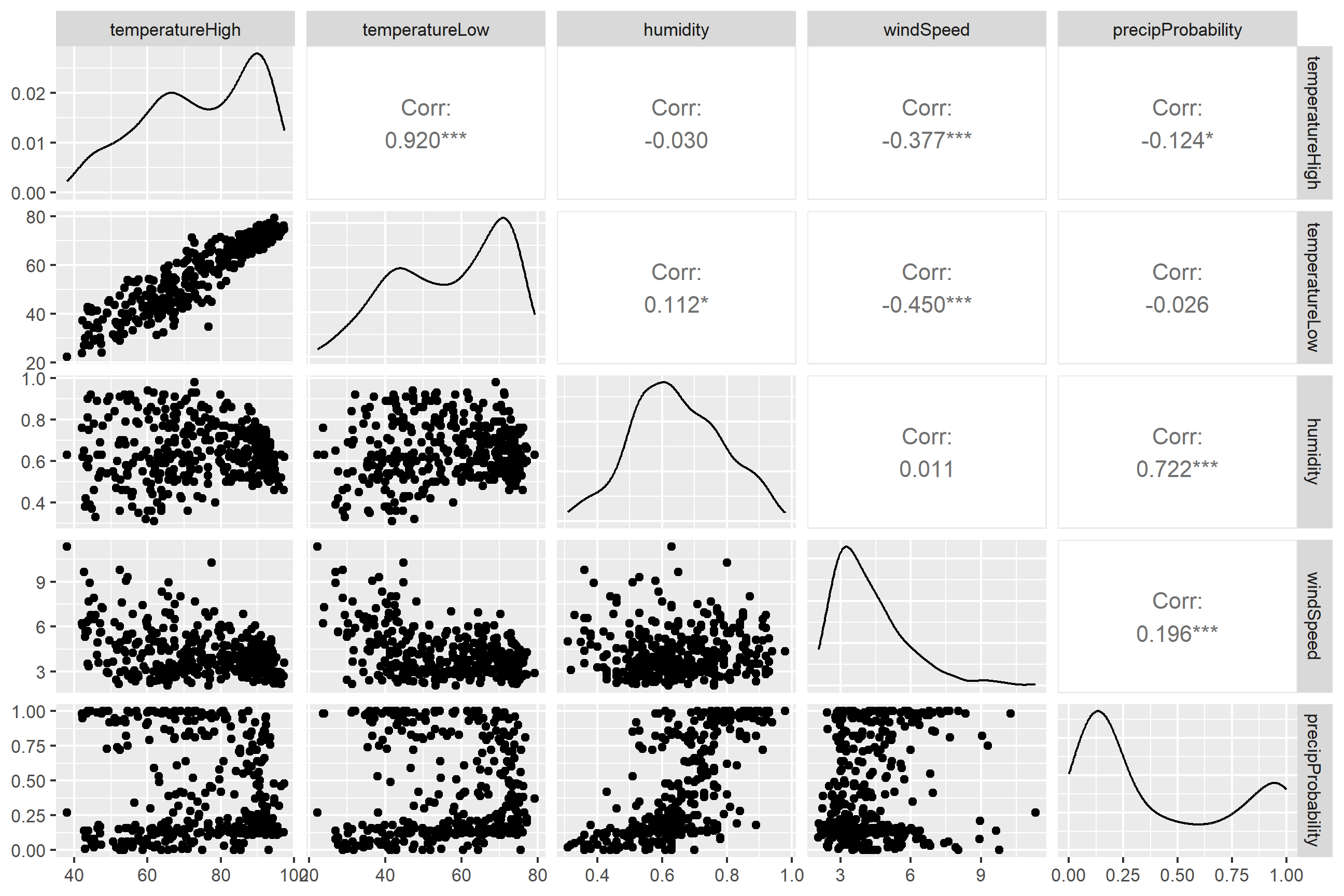
It looks like high and low temperatures are extremely highly positively correlated (r = 0.92). Wind spped and temperature are moderately negatively correlated, with low temperatures having a stronger negative correlation (r = -0.45). There’s no correlation whatsoever between low temperatures and the precipitation probability (r = -0.03) or humidity and high temperatures (r = -0.03).
Even though ggpairs() doesn’t use the standard ggplot(...) + geom_whatever() syntax we’re familiar with, it does behind the scenes, so you can add regular ggplot layers to it:
ggpairs(weather_correlations) +
labs(title = "Correlations!") +
theme_dark()
TRY IT
Make a ggpairs plot for some of the Ames data. You can use str on the data to see which variables might be worth using. Choose 4-5 of them and make a plot.
Correlograms
Scatterplot matrices typically include way too much information to be used in actual publications. I use them when doing my own analysis just to see how different variables are related, but I rarely polish them up for public consumption. In the readings for today, Claus Wilke showed a type of plot called a correlogram which is more appropriate for publication.
These are essentially heatmaps of the different correlation coefficients. To make these with ggplot, we need to do a little bit of extra data processing, mostly to reshape data into a long, tidy format that we can plot. Here’s how.
First we need to build a correlation matrix of the main variables we care about. Ordinarily the cor() function in R takes two arguments—x and y—and it will return a single correlation value. If you feed a data frame into cor() though, it’ll calculate the correlation between each pair of columns. But be careful - don’t feed in hundreds of variables by accident!
# Create a correlation matrix
things_to_correlate <- weather_atl %>%
select(temperatureHigh, temperatureLow, humidity, windSpeed, precipProbability) %>%
cor()
things_to_correlate## temperatureHigh temperatureLow humidity windSpeed precipProbability
## temperatureHigh 1.00 0.920 -0.030 -0.377 -0.124
## temperatureLow 0.92 1.000 0.112 -0.450 -0.026
## humidity -0.03 0.112 1.000 0.011 0.722
## windSpeed -0.38 -0.450 0.011 1.000 0.196
## precipProbability -0.12 -0.026 0.722 0.196 1.000The two halves of this matrix (split along the diagonal line) are identical, so we can remove the lower triangle with this code (which will set all the cells in the lower triangle to NA):
# Get rid of the lower triangle
things_to_correlate[lower.tri(things_to_correlate)] <- NA
things_to_correlate## temperatureHigh temperatureLow humidity windSpeed precipProbability
## temperatureHigh 1 0.92 -0.03 -0.377 -0.124
## temperatureLow NA 1.00 0.11 -0.450 -0.026
## humidity NA NA 1.00 0.011 0.722
## windSpeed NA NA NA 1.000 0.196
## precipProbability NA NA NA NA 1.000Finally, in order to plot this, the data needs to be in tidy (or long) format. Here we convert the things_to_correlate matrix into a data frame, add a column for the row names, take all the columns and put them into a single column named measure1, and take all the correlation numbers and put them in a column named cor In the end, we make sure the measure variables are ordered by their order of appearance (otherwise they plot alphabetically and don’t make a triangle)
things_to_correlate_long <- things_to_correlate %>%
# Convert from a matrix to a data frame
as.data.frame() %>%
# Matrixes have column names that don't get converted to columns when using
# as.data.frame(), so this adds those names as a column
rownames_to_column("measure2") %>%
# Make this long. Take all the columns except measure2 and put their names in
# a column named measure1 and their values in a column named cor
pivot_longer(cols = -measure2,
names_to = "measure1",
values_to = "cor") %>%
# Make a new column with the rounded version of the correlation value
mutate(nice_cor = round(cor, 2)) %>%
# Remove rows where the two measures are the same (like the correlation
# between humidity and humidity)
filter(measure2 != measure1) %>%
# Get rid of the empty triangle
filter(!is.na(cor)) %>%
# Put these categories in order
mutate(measure1 = fct_inorder(measure1),
measure2 = fct_inorder(measure2))
things_to_correlate_long## # A tibble: 10 × 4
## measure2 measure1 cor nice_cor
## <fct> <fct> <dbl> <dbl>
## 1 temperatureHigh temperatureLow 0.920 0.92
## 2 temperatureHigh humidity -0.0301 -0.03
## 3 temperatureHigh windSpeed -0.377 -0.38
## 4 temperatureHigh precipProbability -0.124 -0.12
## 5 temperatureLow humidity 0.112 0.11
## 6 temperatureLow windSpeed -0.450 -0.45
## 7 temperatureLow precipProbability -0.0255 -0.03
## 8 humidity windSpeed 0.0108 0.01
## 9 humidity precipProbability 0.722 0.72
## 10 windSpeed precipProbability 0.196 0.2Phew. With the data all tidied like that, we can make a correlogram with a heatmap. We have manipulated the fill scale a little so that it’s diverging with three colors: a high value, a midpoint value, and a low value.
ggplot(things_to_correlate_long,
aes(x = measure2, y = measure1, fill = cor)) +
geom_tile() +
geom_text(aes(label = nice_cor)) +
scale_fill_gradient2(low = "#E16462", mid = "white", high = "#0D0887",
limits = c(-1, 1)) +
labs(x = NULL, y = NULL, fill = 'Corr.') +
coord_equal() +
theme_minimal() +
theme(panel.grid = element_blank())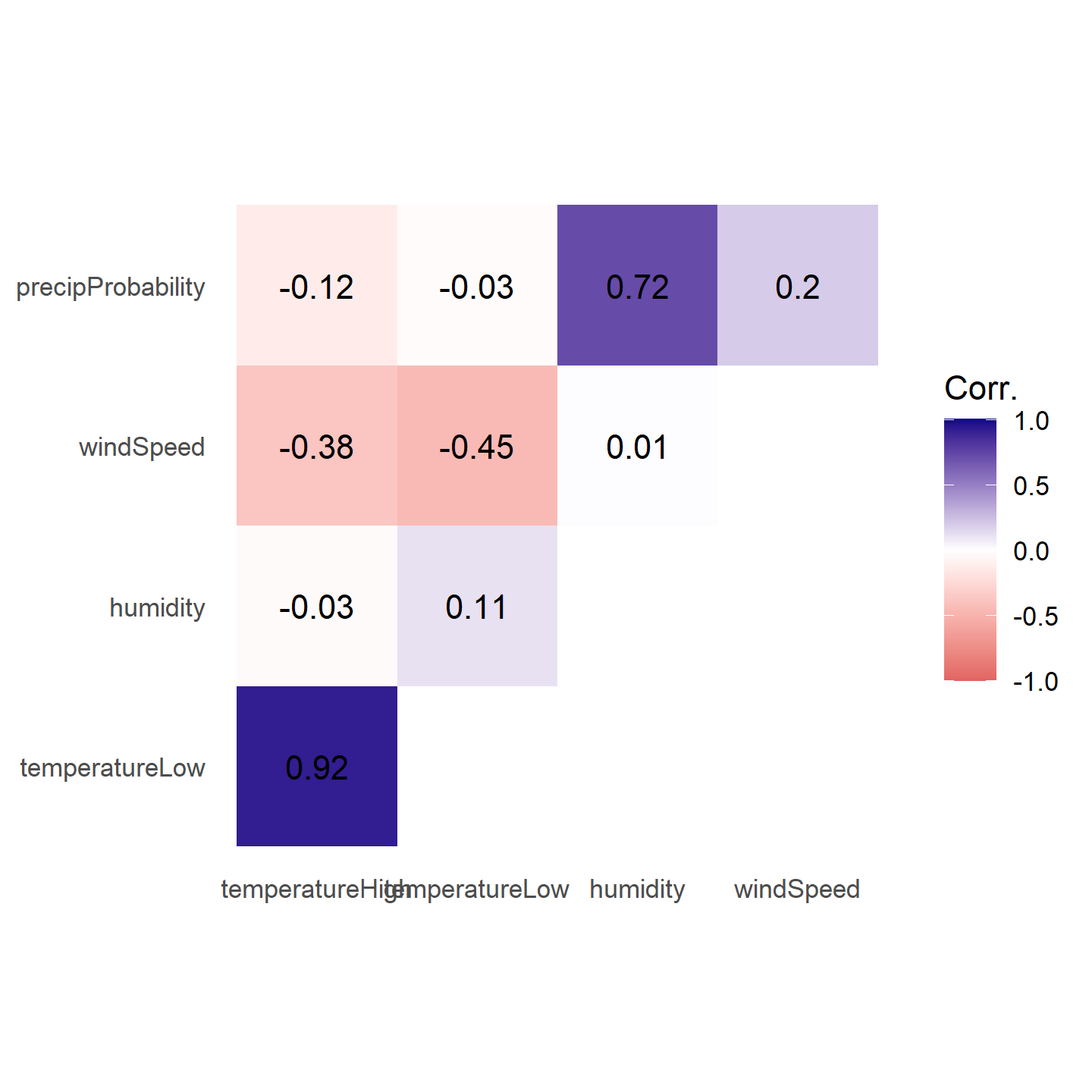
Instead of using a heatmap, we can also use points, which encode the correlation information both as color and as size. To do that, we just need to switch geom_tile() to geom_point() and set the size = cor mapping:
ggplot(things_to_correlate_long,
aes(x = measure2, y = measure1, color = cor)) +
# Size by the absolute value so that -0.7 and 0.7 are the same size
geom_point(aes(size = abs(cor))) +
scale_color_gradient2(low = "#E16462", mid = "white", high = "#0D0887",
limits = c(-1, 1)) +
scale_size_area(max_size = 15, limits = c(-1, 1), guide = 'none') +
labs(x = NULL, y = NULL, color = 'Corr.') +
coord_equal() +
theme_minimal() +
theme(panel.grid.minor = element_blank())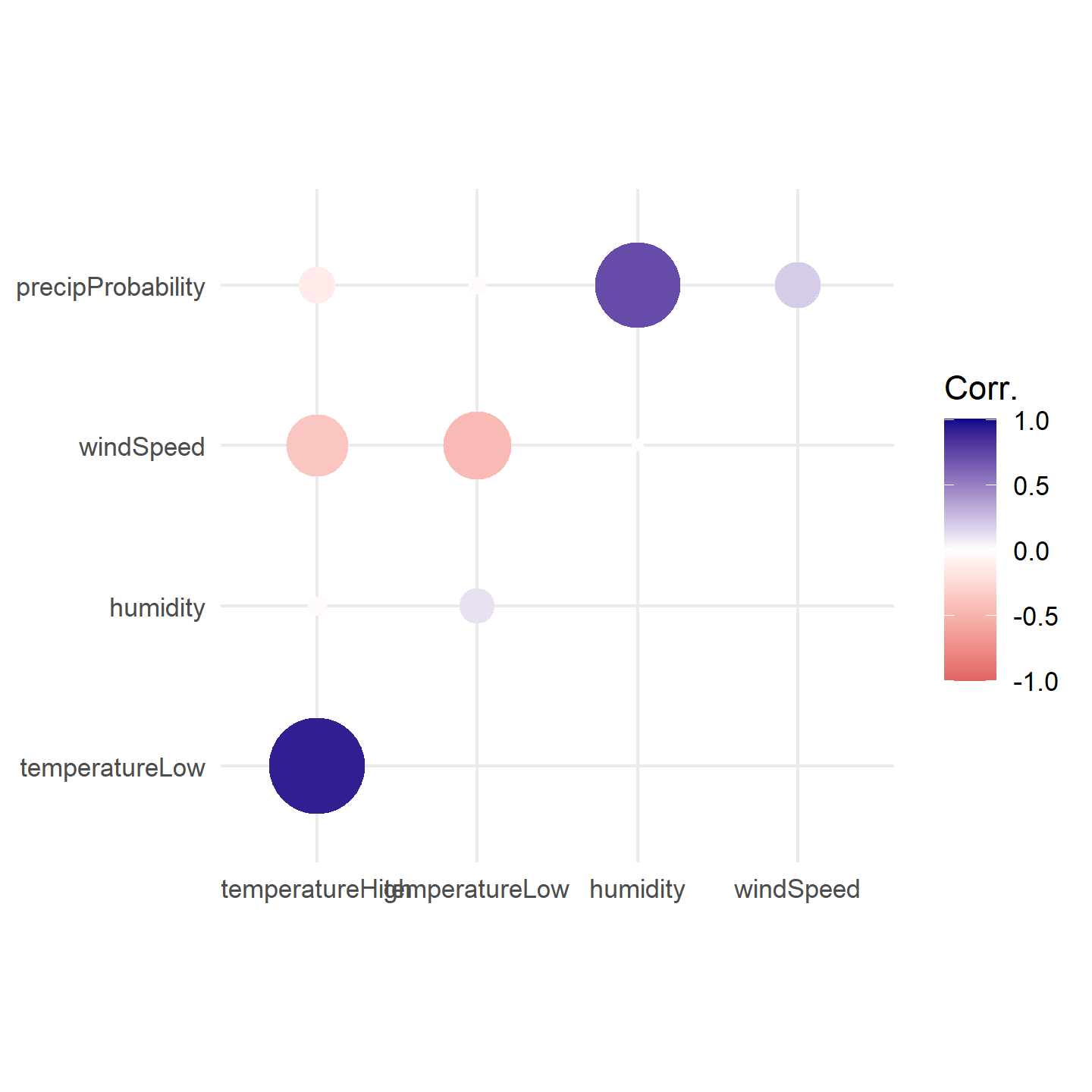
Simple regression
We finally get to this week’s content. Although correlation is nice, we eventually may want to visualize regression. The lecture has shown us some very intuitive, straightforward ways to think about regression (aka, a line). Simple regression is easy to visualize, since you’re only working with an
First, let’s filter the Atlanta weather data to only look at the summer. We also add a column to scale up the humidity value—right now it’s on a scale of 0-1 (for percentages), but when interpreting regression we talk about increases in whole units, so we’d talk about moving from 0% humidity to 100% humidity, which isn’t helpful, so instead we multiply everything by 100 so we can talk about moving from 50% humidity to 51% humidity. We also scale up a couple other variables that we’ll use in the larger model later.
weather_atl_summer <- weather_atl %>%
filter(time >= "2019-05-01", time <= "2019-09-30") %>%
mutate(humidity_scaled = humidity * 100,
moonPhase_scaled = moonPhase * 100,
precipProbability_scaled = precipProbability * 100,
cloudCover_scaled = cloudCover * 100)Then we can build a simple regression model for the high temperature “regressed on” humidity. First, we’ll use the formula from Content 05:
weather_atl_summer %>%
dplyr::summarize(mu_x = mean(humidity_scaled),
mu_y = mean(temperatureHigh),
sd_x = sd(humidity_scaled),
sd_y = sd(temperatureHigh),
rho = sum(((temperatureHigh-mu_y)/sd_y)*((humidity_scaled-mu_x)/sd_x))/(n()-1) ) %>%
# Note in rho we had to use that same "N-1" correction. cor() does this for us automatically
dplyr::mutate(beta_1 = rho*(sd_y/sd_x),
beta_0 = mu_y - beta_1*mu_x)## # A tibble: 1 × 7
## mu_x mu_y sd_x sd_y rho beta_1 beta_0
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 64.8 88.5 10.6 5.33 -0.481 -0.241 104.We can use base-R functions for regression. The workhorse is lm(). To use lm we have to supply:
- The formula for our regression. It starts with the “thing we want to explain” (our “target” or “dependent”) variable, the
~, and then our “explanatory” or “independent” variables.temperatureHigh ~ humidity_scaled.
- Notice we don’t need to say
weather_atl_summer$temperatureHigh. This is because we also supply…
- The data to use. Here
data = weather_atl_summer.
The result will be an lm object. You can use summary(model_simple) to see a summary of results. We’ll use tidy (part of broom which is part of the tidyverse) to convert the results into a tibble:
model_simple <- lm(temperatureHigh ~ humidity_scaled,
data = weather_atl_summer)
tidy(model_simple, conf.int = TRUE)## # A tibble: 2 × 7
## term estimate std.error statistic p.value conf.low conf.high
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 104. 2.35 44.3 1.88e-88 99.5 109.
## 2 humidity_scaled -0.241 0.0358 -6.74 3.21e-10 -0.312 -0.170We can interpret these coefficients like so:
The intercept, by definition of an intercept, shows that the average temperature when there’s 0% humidity is 104°. There are no days with 0% humidity though, so we can ignore the intercept—it’s really just here so that we can draw the line.
The coefficient for
humidity_scaledshows that a one percent increase in humidity is associated with a 0.241° decrease in temperature, on average.- The 95% confidence interval (remember, this slope coefficient is a random variable) does not include zero.
Visualizing this model is simple, since there are only two variables:
ggplot(weather_atl_summer,
aes(x = humidity_scaled, y = temperatureHigh)) +
geom_point() +
geom_smooth(method = "lm")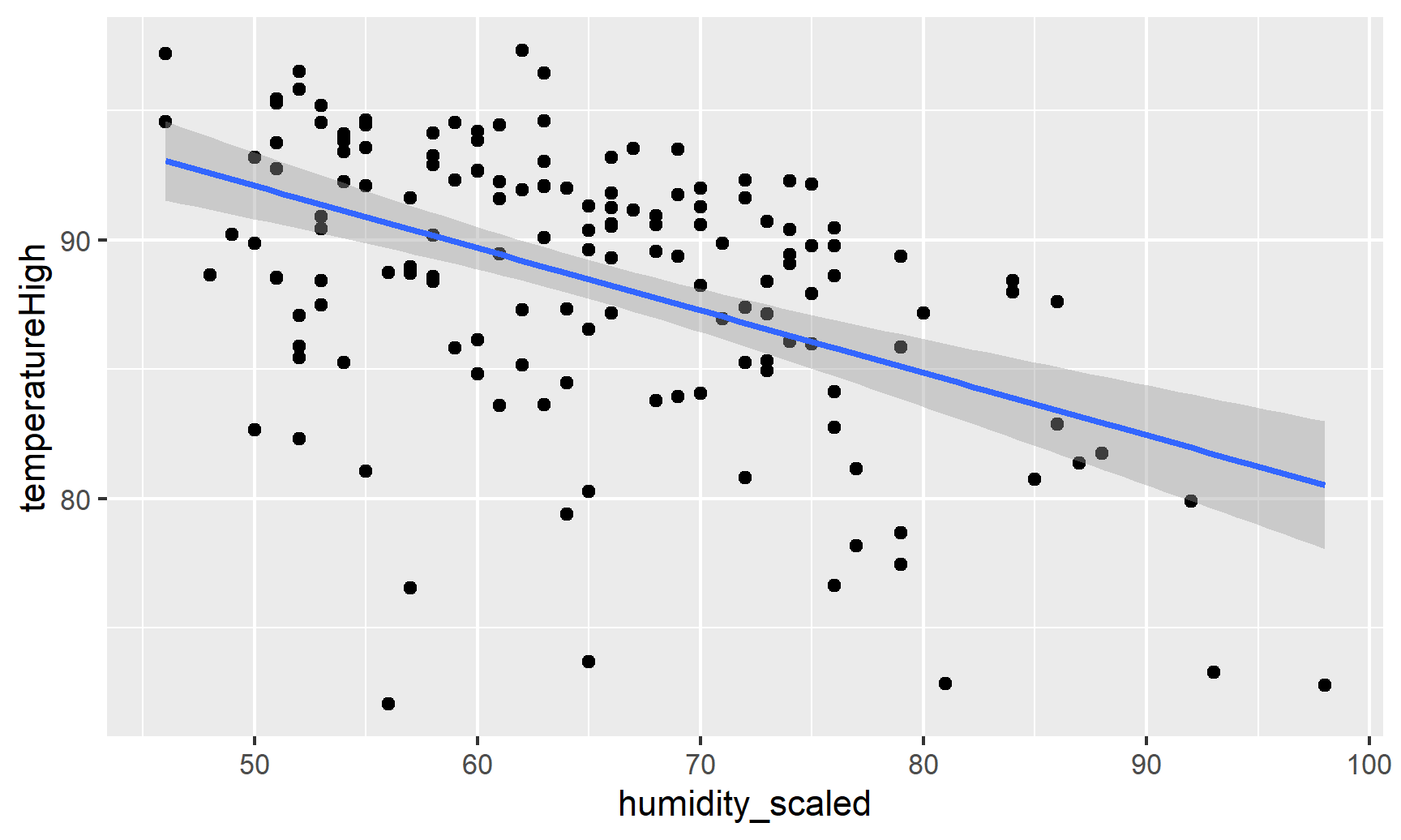
And indeed, as humidity increases, temperatures mostly decrease.
Coefficient plots
But if we use multiple variables in the model (and we will do this a lot going forward), it gets really hard to visualize the results since we’re working with multiple dimensions. Instead, we can use coefficient plots to see the individual coefficients in the model.
First, let’s build a more complex model, where “complex” is defined as “more things explaining our outcome, high temp”:
model_complex <- lm(temperatureHigh ~ humidity_scaled + moonPhase_scaled +
precipProbability_scaled + windSpeed + pressure + cloudCover_scaled,
data = weather_atl_summer)
tidy(model_complex, conf.int = TRUE)## # A tibble: 7 × 7
## term estimate std.error statistic p.value conf.low conf.high
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 262. 125. 2.09 0.0380 14.8 510.
## 2 humidity_scaled -0.111 0.0757 -1.47 0.143 -0.261 0.0381
## 3 moonPhase_scaled 0.0116 0.0126 0.917 0.360 -0.0134 0.0366
## 4 precipProbability_scaled 0.0356 0.0203 1.75 0.0820 -0.00458 0.0758
## 5 windSpeed -1.78 0.414 -4.29 0.0000326 -2.59 -0.958
## 6 pressure -0.157 0.122 -1.28 0.203 -0.398 0.0854
## 7 cloudCover_scaled -0.0952 0.0304 -3.14 0.00207 -0.155 -0.0352We can interpret these coefficients like so:
- Holding everything else constant, a 1% increase in humidity is associated with a 0.11° decrease in the high temperature, on average, but the effect is not statistically significant
- Holding everything else constant, a 1% increase in moon visibility is associated with a 0.01° increase in the high temperature, on average, and the effect is not statistically significant
- Holding everything else constant, a 1% increase in the probability of precipitation is associated with a 0.04° increase in the high temperature, on average, and the effect is not statistically significant
- Holding everything else constant, a 1 mph increase in the wind speed is associated with a 1.8° decrease in the high temperature, on average, and the effect is statistically significant
- Holding everything else constant, a 1 unit increase in barometric pressure is associated with a 0.15° decrease in the high temperature, on average, and the effect is not statistically significant
- Holding everything else constant, a 1% increase in cloud cover is associated with a 0.01° decrease in the high temperature, on average, and the effect is statistically significant
- The intercept is pretty useless. It shows that the predicted temperature will be 262° when humidity is 0%, the moon is invisible, there’s no chance of precipitation, no wind, no barometric pressure, and no cloud cover. Yikes.
To plot all these things at once, we’ll store the results of tidy(model_complex) as a data frame, remove the useless intercept, and plot it using geom_pointrange():
model_tidied <- tidy(model_complex, conf.int = TRUE) %>%
filter(term != "(Intercept)")
ggplot(model_tidied,
aes(x = estimate, y = term)) +
geom_vline(xintercept = 0, color = "red", linetype = "dotted") +
geom_pointrange(aes(xmin = conf.low, xmax = conf.high)) +
labs(x = "Coefficient estimate", y = NULL) +
theme_minimal()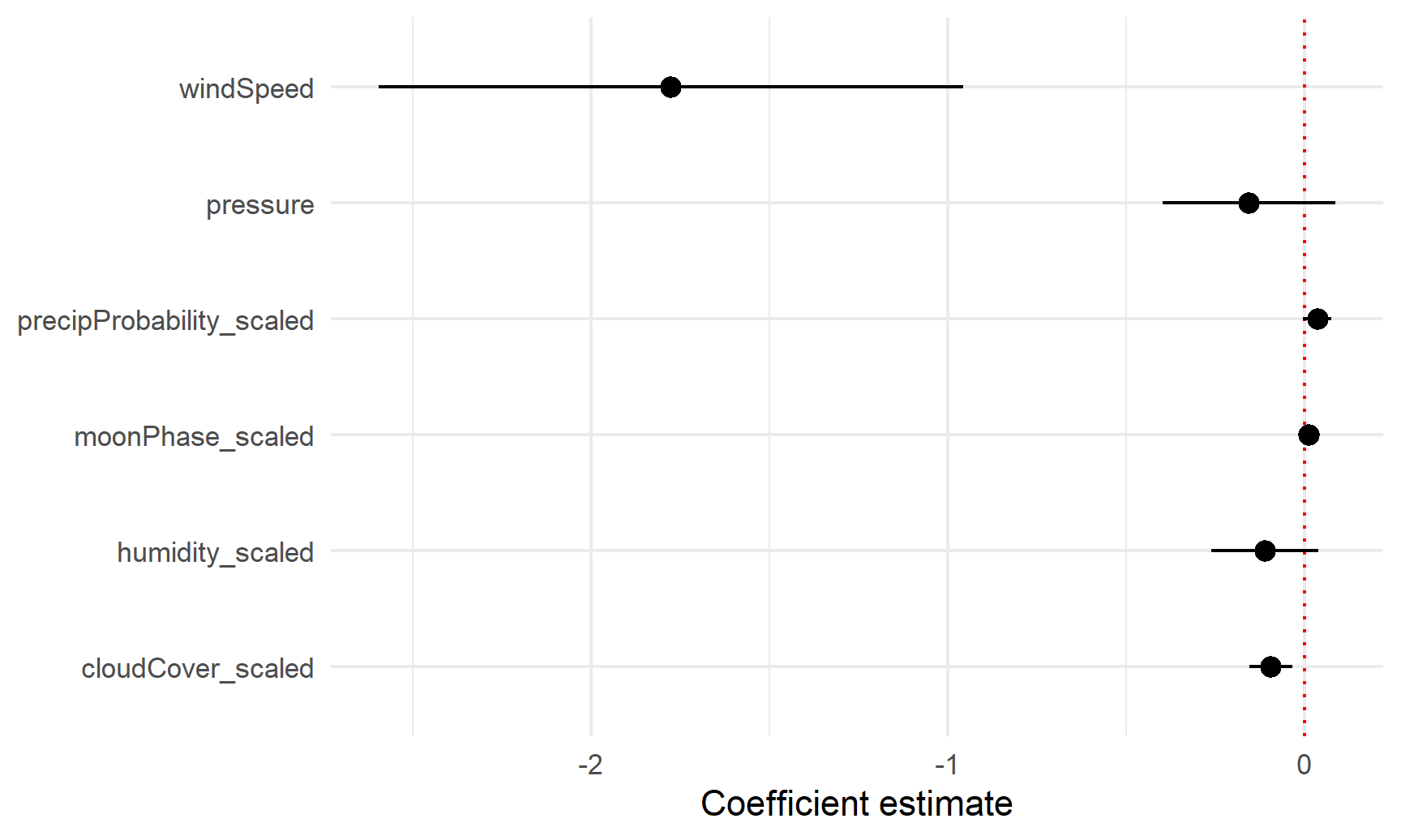
Neat! Now we can see how big these different coefficients are and how close they are to zero. Wind speed has a big significant effect on temperature. The others are all very close to zero.
Marginal effects plots
Instead of just looking at the coefficients, we can also see the effect of moving different variables up and down like sliders and switches. Remember that regression coefficients allow us to build actual mathematical formulas that predict the value of Y. The coefficients from model_compex yield the following big hairy ugly equation:
If we plug in values for each of the explanatory variables, we can get the predicted expected value of high temperature, or
The augment() function in the broom library allows us to take a data frame of explanatory variable values, plug them into the model equation, and get predictions out. For example, let’s set each of the variables to some arbitrary values (50% for humidity, moon phase, chance of rain, and cloud cover; 1000 for pressure, and 1 MPH for wind speed).
newdata_example <- tibble(humidity_scaled = 50, moonPhase_scaled = 50,
precipProbability_scaled = 50, windSpeed = 1,
pressure = 1000, cloudCover_scaled = 50)
newdata_example## # A tibble: 1 × 6
## humidity_scaled moonPhase_scaled precipProbability_scaled windSpeed pressure cloudCover_scaled
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 50 50 50 1 1000 50We can plug these values into the model with augment():
# I use select() here because augment() returns columns for all the explanatory
# variables, and the .fitted column with the predicted value is on the far right
# and gets cut off
augment(model_complex, newdata = newdata_example, se_fit=TRUE) %>%
select(.fitted, .se.fit)## # A tibble: 1 × 2
## .fitted .se.fit
## <dbl> <dbl>
## 1 96.2 3.19Given these weather conditions, the predicted high temperature is 96.2°. Now you’re an armchair meteorologist!
We can follow the same pattern to show how the predicted temperature changes as specific variables change across a whole range. Here, we create a data frame of possible wind speeds and keep all the other explanatory variables at their means:
newdata <- tibble(windSpeed = seq(0, 8, 0.5),
pressure = mean(weather_atl_summer$pressure),
precipProbability_scaled = mean(weather_atl_summer$precipProbability_scaled),
moonPhase_scaled = mean(weather_atl_summer$moonPhase_scaled),
humidity_scaled = mean(weather_atl_summer$humidity_scaled),
cloudCover_scaled = mean(weather_atl_summer$cloudCover_scaled))
newdata## # A tibble: 17 × 6
## windSpeed pressure precipProbability_scaled moonPhase_scaled humidity_scaled cloudCover_scaled
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 0 1016. 40.2 50.7 64.8 29.5
## 2 0.5 1016. 40.2 50.7 64.8 29.5
## 3 1 1016. 40.2 50.7 64.8 29.5
## 4 1.5 1016. 40.2 50.7 64.8 29.5
## 5 2 1016. 40.2 50.7 64.8 29.5
## 6 2.5 1016. 40.2 50.7 64.8 29.5
## 7 3 1016. 40.2 50.7 64.8 29.5
## 8 3.5 1016. 40.2 50.7 64.8 29.5
## 9 4 1016. 40.2 50.7 64.8 29.5
## 10 4.5 1016. 40.2 50.7 64.8 29.5
## 11 5 1016. 40.2 50.7 64.8 29.5
## 12 5.5 1016. 40.2 50.7 64.8 29.5
## 13 6 1016. 40.2 50.7 64.8 29.5
## 14 6.5 1016. 40.2 50.7 64.8 29.5
## 15 7 1016. 40.2 50.7 64.8 29.5
## 16 7.5 1016. 40.2 50.7 64.8 29.5
## 17 8 1016. 40.2 50.7 64.8 29.5If we feed this big data frame into augment(), we can get the predicted high temperature for each row. We can also use the .se.fit column to calculate the 95% confidence interval for each predicted value. We take the standard error, multiply it by -1.96 and 1.96 (or the quantile of the normal distribution at 2.5% and 97.5%), and add that value to the estimate.
predicted_values <- augment(model_complex, newdata = newdata, se_fit=TRUE) %>%
mutate(conf.low = .fitted + (-1.96 * .se.fit),
conf.high = .fitted + (1.96 * .se.fit))
predicted_values %>%
select(windSpeed, .fitted, .se.fit, conf.low, conf.high) %>%
head()## # A tibble: 6 × 5
## windSpeed .fitted .se.fit conf.low conf.high
## <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 0 95.3 1.63 92.2 98.5
## 2 0.5 94.5 1.42 91.7 97.2
## 3 1 93.6 1.22 91.2 96.0
## 4 1.5 92.7 1.03 90.7 94.7
## 5 2 91.8 0.836 90.1 93.4
## 6 2.5 90.9 0.653 89.6 92.2Cool! Just looking at the data in the table, we can see that predicted temperature drops as windspeed increases. We can plot this to visualize the effect:
ggplot(predicted_values, aes(x = windSpeed, y = .fitted)) +
geom_ribbon(aes(ymin = conf.low, ymax = conf.high),
fill = "#BF3984", alpha = 0.5) +
geom_line(size = 1, color = "#BF3984") +
labs(x = "Wind speed (MPH)", y = "Predicted high temperature (F)") +
theme_minimal()## Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
## ℹ Please use `linewidth` instead.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was generated.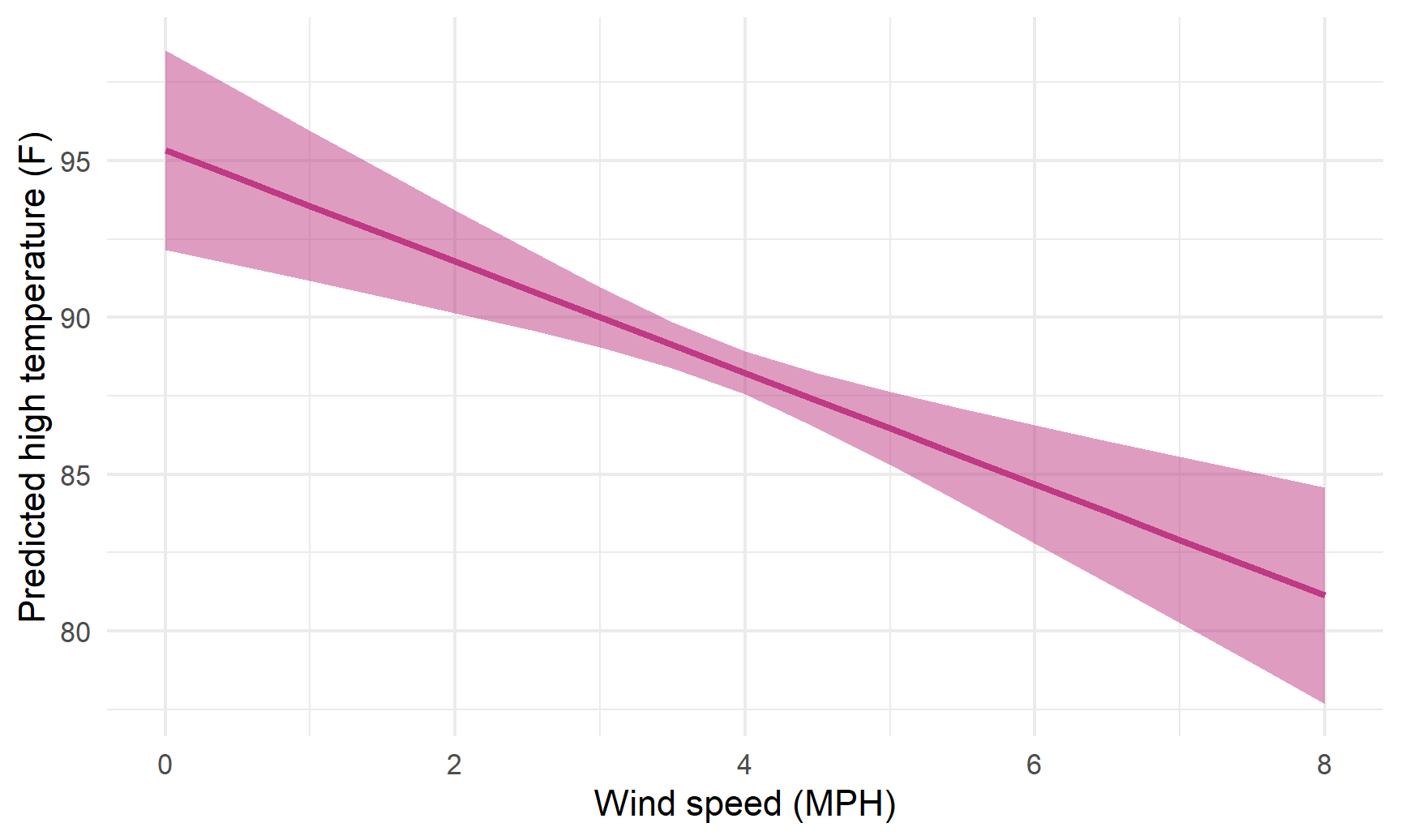
We just manipulated one of the model coefficients and held everything else at its mean. We can manipulate multiple variables too and encode them all on the graph. For instance, what is the effect of windspeed and cloud cover on the temperature?
We’ll follow the same process, but vary both windSpeed and cloudCover_scaled. Instead of using tibble(), we use exapnd_grid(), which creates every combination of the variables we specify. Instead of varying cloud cover by every possible value (like from 0 to 100), we’ll choose four possible cloud cover types: 0%, 33%, 66%, and 100%. Everything else will be at its mean.
newdata_fancy <- expand_grid(windSpeed = seq(0, 8, 0.5),
pressure = mean(weather_atl_summer$pressure),
precipProbability_scaled = mean(weather_atl_summer$precipProbability_scaled),
moonPhase_scaled = mean(weather_atl_summer$moonPhase_scaled),
humidity_scaled = mean(weather_atl_summer$humidity_scaled),
cloudCover_scaled = c(0, 33, 66, 100))
newdata_fancy## # A tibble: 68 × 6
## windSpeed pressure precipProbability_scaled moonPhase_scaled humidity_scaled cloudCover_scaled
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 0 1016. 40.2 50.7 64.8 0
## 2 0 1016. 40.2 50.7 64.8 33
## 3 0 1016. 40.2 50.7 64.8 66
## 4 0 1016. 40.2 50.7 64.8 100
## 5 0.5 1016. 40.2 50.7 64.8 0
## 6 0.5 1016. 40.2 50.7 64.8 33
## 7 0.5 1016. 40.2 50.7 64.8 66
## 8 0.5 1016. 40.2 50.7 64.8 100
## 9 1 1016. 40.2 50.7 64.8 0
## 10 1 1016. 40.2 50.7 64.8 33
## # ℹ 58 more rowsNotice now that windSpeed repeats four times (0, 0, 0, 0, 0.5, 0.5, etc.), since there are four possible cloudCover_scaled values (0, 33, 66, 100).
We can plot this now, just like before, with wind speed on the x-axis, the predicted temperature on the y-axis, and colored and faceted by cloud cover:
predicted_values_fancy <- augment(model_complex, newdata = newdata_fancy, se_fit=TRUE) %>%
mutate(conf.low = .fitted + (-1.96 * .se.fit),
conf.high = .fitted + (1.96 * .se.fit)) %>%
# Make cloud cover a categorical variable
mutate(cloudCover_scaled = factor(cloudCover_scaled))
ggplot(predicted_values_fancy, aes(x = windSpeed, y = .fitted)) +
geom_ribbon(aes(ymin = conf.low, ymax = conf.high, fill = cloudCover_scaled),
alpha = 0.5) +
geom_line(aes(color = cloudCover_scaled), size = 1) +
labs(x = "Wind speed (MPH)", y = "Predicted high temperature (F)") +
theme_minimal() +
guides(fill = 'none', color = 'none') +
facet_wrap(vars(cloudCover_scaled), nrow = 1)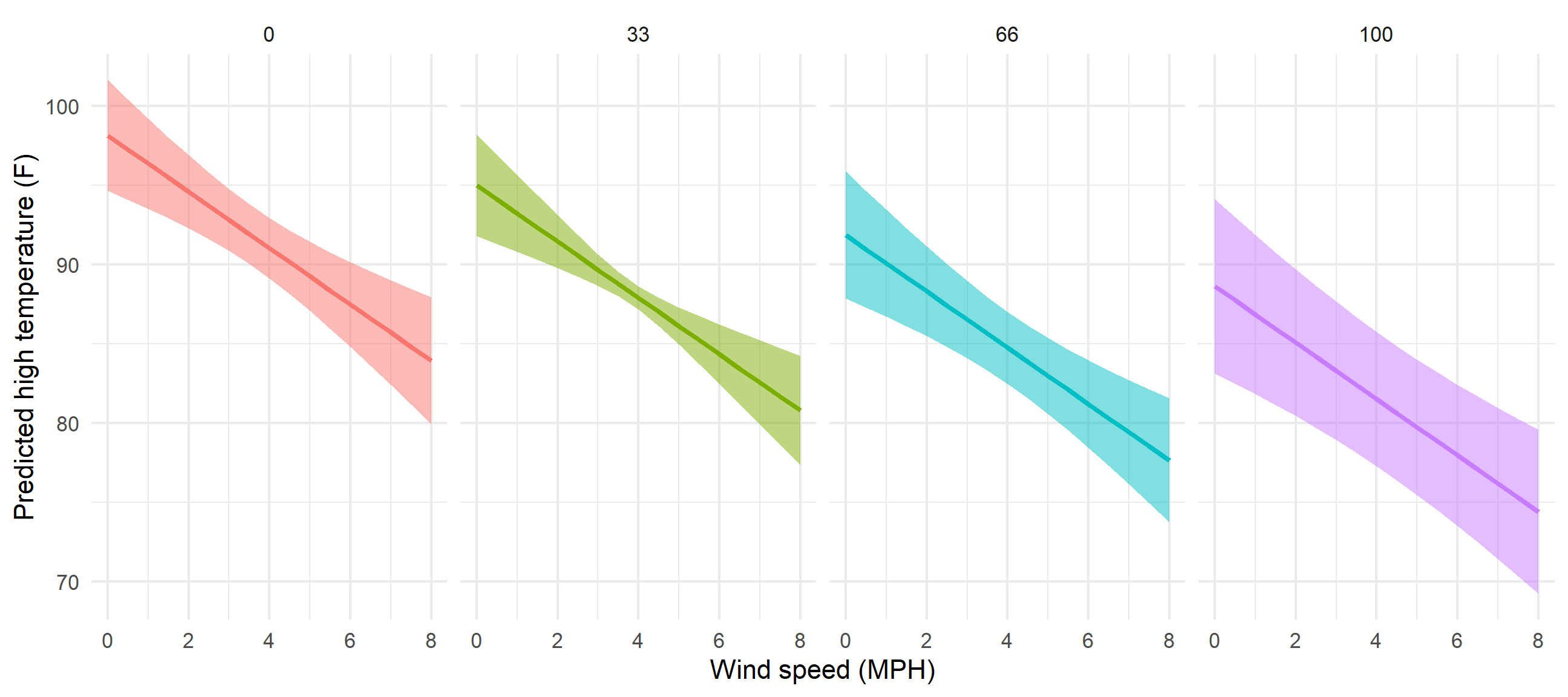
Nice. Temperatures go down slightly as cloud cover increases. If we wanted to improve the model, we’d add an interaction term between cloud cover and windspeed so that each line would have a different slope in addition to a different intercept, but that’s beyond the scope of this class.